Avatar

Office - MC 6028

smelczer (at) uwaterloo.ca

1-519-888-4567 x41282

I’m an assistant professor in the Department of Combinatorics and Optimization at the University of Waterloo (with a cross-appointment in the School of Computer Science), interested in leveraging computational algebraic geometry, analysis, and topology to create effective tools for combinatorics, computer science, and mathematics.

An overview of some of my research interests can be found in the first chapter of An Invitation to Enumeration. More details can be found on my research page.

Previously I was a CRM-ISM postdoctoral fellow at UQAM (2019 – 2020) and a postdoc at the University of Pennsylvania (2017 – 2019). I received doctorates from the École normale supérieure de Lyon and the University of Waterloo in 2017.

I’ve written two textbooks,

The first textbook is an introduction to analytic combinatorics in several variables, suitable for graduate students and those new to the area, while the second is a more advanced treatment making extensive use of homology, multivariate residues, and similar constructions.

See also my notes on enumeration.ca for an elementary introduction to enumerative combinatorics.

News / Events

Analytic Combinatorics in Several Variables, 2nd Edition OUT NOW

Published February 2024

FPSAC 2025 (Plenary Speaker), July 2025

At Hokkaido University, Japan

AofA 2025 (Organizing Committee Co-Chair), May 2025

At the Fields Institute, Toronto

Joined AofA Steering Committee, June 2024

Next events in Toronto (2025) and Munich (2026)

Jeremy Chizewer wins 2024 Governor General Gold Medal

Congratulations Jeremy!

AofA 2024 (Program Committee), June 2024

At the University of Bath, UK

An Invitation to Analytic Combinatorics hits 11k chapter downloads

On SpringerLink digital service (not including hard copies sold)


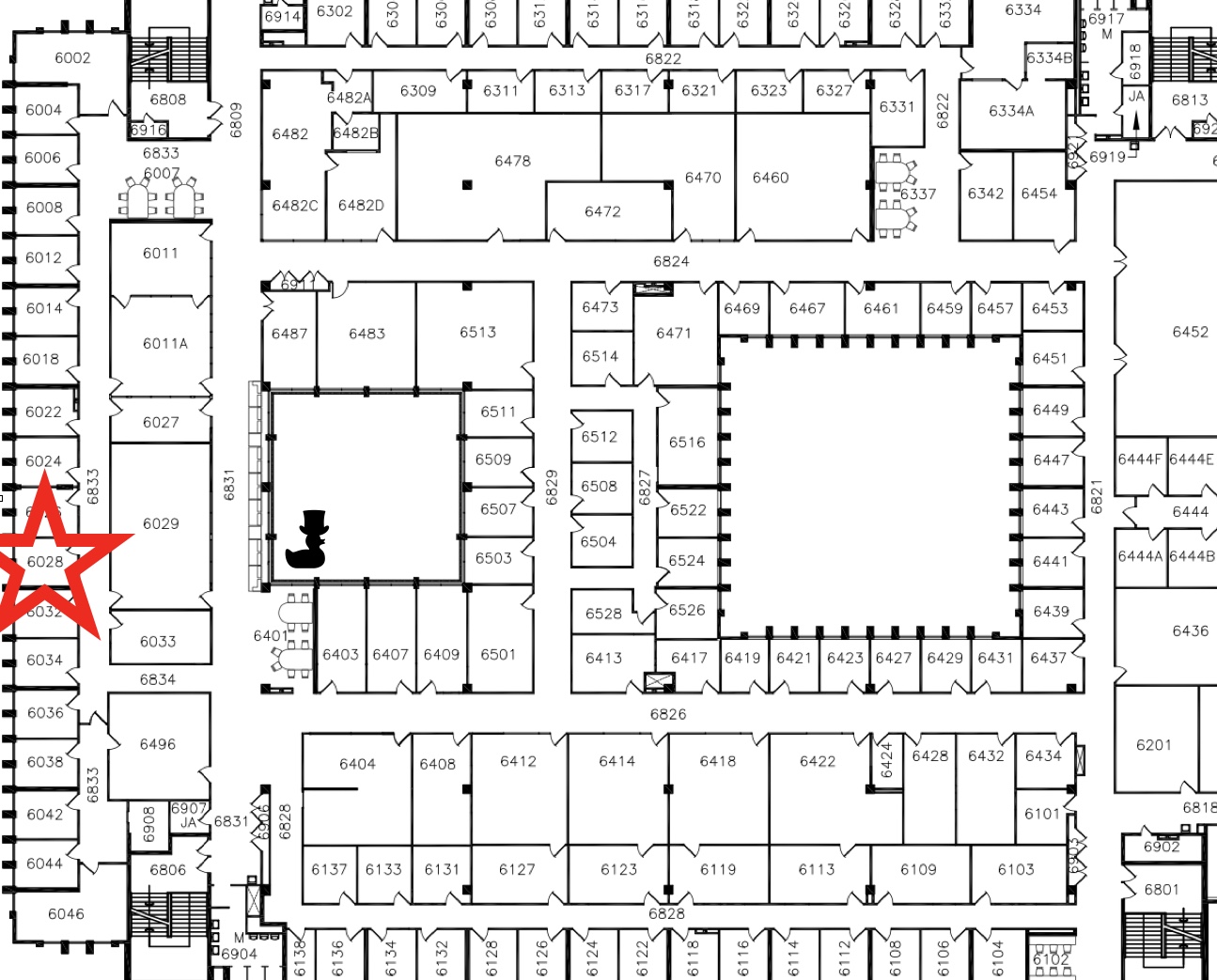
Map to Office

My office is MC 6028 (click for a larger version).

Coauthors

Yuliy Baryshnikov, Alin Bostan, Mireille Bousquet-Mélou, Sophie Burrill, Jeremy Chizewer, Julien Courtiel, Ruiwen Dong, Éric Fusy, Torin Greenwood, Benjamin Hackl, Kevin Hyun, Veronika Irvine, Manuel Kauers, Jessica Khera, Alexander Kroitor, Kisun Lee, Andreas Lenz, Erik Lundberg, Andrew Luo, Marc Mezzarobba, Marcus Michelen, Marni Mishna, Somabha Mukherjee, J. Ian Munro, Greta Panova, Robin Pemantle, Ava Pun, Kilian Raschel, Cyrus Rashtchian, Frank Ruskey, Tiadora Ruza, Bruno Salvy, Éric Schost, Jesse Selover, Paul H. Siegel, Josip Smolčić, Catherine St-Pierre, Armin Straub, Mark Wilson, Elaine Wong