Example 7.1 (Automated Apéry Asymptotics)
This worksheet requires the DiagonalAsymptotics/Kronecker package available at http://diagasympt.gforge.inria.fr 

>	# Import Kronecker package read "Kronecker.mpl"; # Define the rational function F := 1/(1-w*(1+x)*(1+y)*(1+z)*(1+y+z+y*z+x*y*z)); # Compute dominant asymptotics of the main power series diagonal A, U := DiagonalAsymptotics(numer(F),denom(F),[w,x,y,z],u,n):

 

(1)

 

>	# Asymptotics are represented by the symbolic expression A;

 

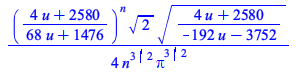(2)

 

>	# When u takes the following value # Note 1: The large numeric precision was used to verify minimality # Note 2: Random choices are used to output this result. Rerun the code to get #         different expressions! (which yield the same asymptotic behaviour, of course) U;

 

(3)

 

>	# Because u is an algebraic number of degree two in this example, we can express asymptotic behaviour exactly evala(allvalues(subs(u=U[1],A)));

 

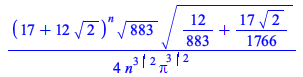(4)

 

>