Example 2.16 (The Connection Problem for Supertrees) 

with(gfun): 

>

 

>	# Enter the algebraic equations for the generating function of supertrees P := y^4-2*y^3+(1+2*z)*y^2-2*z*y+4*z^3;

 

(1)

 

>	# Plot the branches y(z) defined by P(z,y) = 0 r1,r2,r3,r4 := solve(P,y,explicit): plot([r1,r2,r3,r4],z=-0.5..0.3, thickness=5);

 

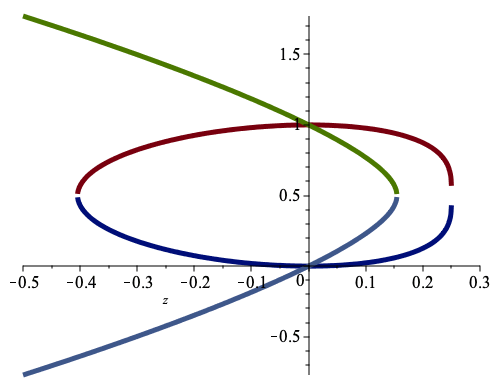>	# The singularities are the roots of the discriminant of P with respect to y disc := factor(discrim(P,y));

 

(2)

 

>	# Thus the dominant singularity of the generating function is one of these points # Pringsheim's theorem implies the dominant singularity is real and positive sing := sort([solve(disc,dropmultiplicity=true)]): sing = evalf(sing);

 

(3)

 

>	# These are series expansions of solutions at the origin # NOTE: The branches may change order when running the code P1,P2,P3,P4 := op(algeqtoseries(P,z,y,5)): 'P1' = P1; 'P2' = P2; 'P3' = P3; 'P4' = P4;

 

 

 

 

	(4)

 

>	# These are series expansions of solutions at z=rho -- here t = 1-z/rho rho := sqrt(5)/8 - 1/8: Q1,Q2,Q3,Q4 := op({seq(op(k),k=[allvalues(algeqtoseries(subs(z=rho-rho*t,P),t,y,2))])}): Q1,Q2,Q3,Q4 := simplify(Q1),simplify(Q2),simplify(Q3),simplify(Q4): 'Q1' = Q1; 'Q2' = Q2; 'Q3' = Q3; 'Q4' = Q4;

 

 

 

 

	(5)

 

>	# These are series expansions of solutions at z=1/4 -- here s = 1-4z R1,R2,R3,R4 := op({seq(op(k),k=[allvalues(algeqtoseries(subs(z=1/4-s/4,P),s,y,5))])}): 'R1' = R1; 'R2' = R2; 'R3' = R3; 'R4' = R4;

 

 

 

 

	(6)

 

>	# As described in the textbook, sorting the real branches to the left and right of each point, using these expansions, allows one to get the singular expansion of the bicoloured supertree generating function near its dominant singularity

 

>

 

>

 

>