Example 2.17 (Kreweras Lattice Walks) 

with(gfun):
 

>

# The minimal polynomial listed can be proven using the kernel method. # Here we heuristically guess the minimal polynomial using gfun. # This takes up to 30 seconds. # Generate terms in the counting sequence KrewWalksIJ := proc(n,i,j)  option remember:  if i < 0 or j < 0 then return 0:  elif n=0 and i=0 and j=0 then return 1:  elif n=0 then return 0:  else return KrewWalksIJ(n-1,i+1,j) + KrewWalksIJ(n-1,i,j+1) + KrewWalksIJ(n-1,i-1,j-1):  end if: end: KrewWalks := proc(n)  return add(add(KrewWalksIJ(n,i,j),i=0..n),j=0..n): end: # Generate counting sequence LST := [seq(KrewWalks(k),k=0..100)]: P := subs(y(z)=y,listtoalgeq(LST,y(z))[1]);

 

(1)

 

>	# Plot part of the real algebraic curve defined by P plots[implicitplot](P,z=-10..10,y=-30..30);

 

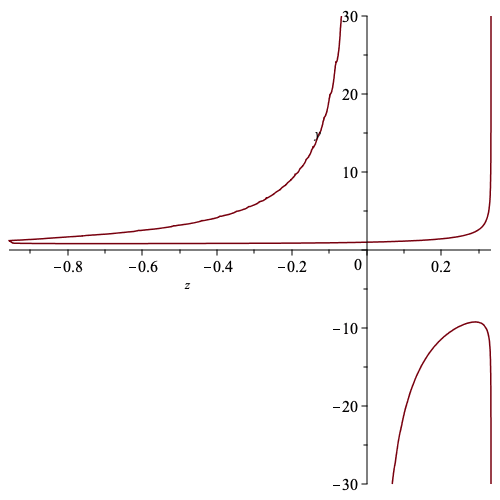>	# Find potential singularities of the generating function factor(discrim(P,y)*coeff(P,y,6));

 

(2)

 

>	# Solutions to P(z,y) at the origin algeqtoseries(P,z,y,3);

 

(3)

 

>	# Solutions to P(z,y) around dominant singularity z = 1/3 algeqtoseries(subs(z=(1-t)/3,P),t,y,3): subs(t=1-3*z,%);

 

(4)

 

>	# There are two real solutions beginning +/- 2*sqrt(2)*(1-3*z)^(-1/4) + ... # Thus f(z) ~ 2*sqrt(2)*(1-3*z)^(-1/4), giving dominant asymptotics ASM := 3^n * 2*sqrt(2) * n^(-3/4) / GAMMA(1/4);

 

(5)

 

>	# Heuristically check that our asymptotic is close to the actual sequence value PR := rectoproc(listtorec(LST,u(n))[1],u(n)): evalf(PR(1000)/subs(n=1000,ASM));

 

(6)

 

>