Examples 2.8, 2.9, 2.10, and 2.12 (Puiseux Expansions of Rooted Binary and 3-Ary Trees) 

with(gfun): 

>

 

>	# Enter the algebraic equations for the generating functions under consideration P2 := z*y^2-y+1; P3 := z*y^3-y+1;

 

 

	(1)

 

>	# There are two Puiseix series solutions to the equation for binary trees algeqtoseries(P2,z,y,5);

 

(2)

 

>	# There are three Puiseix series solutions to the equation for 3-ary trees # By default, the RootOf data structure is used to encode algebraic quantities algeqtoseries(P3,z,y,5);

 

(3)

 

>	# The allvalues command can be used to represent these expansions explicitly allvalues(algeqtoseries(P3,z,y,5));

 

(4)

 

>	# Compute expansions in t = 1-4z around the singular point z=1/4 allvalues(algeqtoseries(subs(z=(1-t)/4,P2),t,y,5));

 

(5)

 

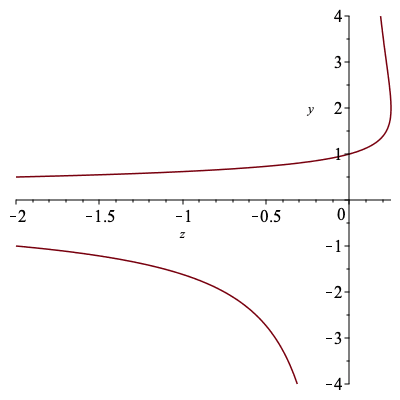
>	# The algebraic curves defined by the algebraic equation for binary trees have singularities at the origin and z=1/4 {solve(discrim(P2,y))}, {solve(lcoeff(P2,y))};

 

(6)

 

>	# There is a branch going to infinity at 0 and two branches colliding at 1/4 plots[implicitplot](P2,z=-2..2,y=-4..4, numpoints=10^4);

 

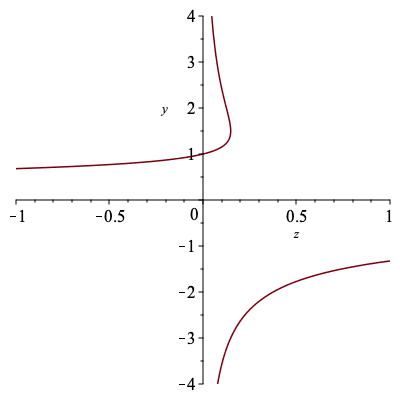
>	# The algebraic curves defined by the algebraic equation for 3-ary trees have singularities at the origin and z=4/27 {solve(discrim(P3,y))}, {solve(lcoeff(P3,y))};

 

(7)

 

>	# There are branches going to infinity at 0 and two branches colliding at 1/4 # (One can also imagine two branches colliding "at infinity" as z goes to 0) plots[implicitplot](P3,z=-1..1,y=-4..4, numpoints=10^4);

 

>