Example 4.1 (One Dimensional Excursions) 

with(gfun): 

>

 

>	# Define the set of steps and kernel ST := [-2,-1,0,1,2]: K := 1-t*add(x^k,k=ST);

 

(1)

 

>	# As expected, two solutions of K are finite near the origin and two go to +/- infinity ser := ListTools[Flatten]([allvalues(algeqtoseries(numer(K),t,x,5))]): for k in ser do: k od;

 

 

 

 

	(2)

 

>	# We take the small roots, which are degree four algebraic numbers rts := map(evala,[solve(K,x,explicit)]): r1,r2 := op(select(r->limit(r,t=0,right)=0,rts));

 

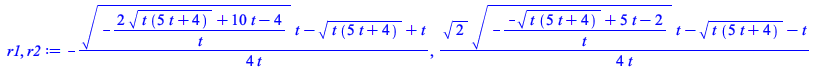(3)

 

>	# The generating function is then given explicitly E := evala(t*diff(r1,t)/r1 + t*diff(r2,t)/r2) assuming t>0: series(E,t,8) assuming t>0;

 

(4)

 

>	# To derive the minimal polynomial of E, we start with P such that P(r1,t) = P(r2,t) = 0 P := numer(K);

 

(5)

 

>	# The chain rule gives poly Pd(d,t) such that P(r1'(t),t) = P(r2'(t),t) = 0 dpol := subs(diff(r(t), t)=d,r(t)=x, diff(subs(x=r(t),P),t)); Pd := resultant(P,dpol,x); evala(subs(d=diff(r1,t),Pd));

 

 

 

	(6)

 

>

# The quantities r1'/r1 and r2'/r2 are a root in y of the resultant of P(z,t) and Pd(z*y,t) # We then scale y -> y/t since we want to add res := factor(subs(y=y/t,resultant(subs(x=z,P),subs(d=y*z,Pd),z))): # The resultant is large degree and has three factors # We use the starting series terms of t*r1'/r1 to determine which factor we want serstart := convert(series(t*diff(r1,t)/r1,t,10),polynom) assuming t>0: poss_minpol := [seq(k[1], k=sqrfree(res)[2])]: Pquo := op(select(p->convert(series(subs(y=serstart,p),t,5),polynom)=0,poss_minpol));

 

(7)

 

>

# The generating function E = t*r1'/r1 + t*r2'/r2 is then a root of the resultant of P(y,t) and P(e-y,t) in y res2 := factor(resultant(Pquo,subs(y=e-y,Pquo),y)): # Again we factor and use starting series terms to determine the minimal polynomial serstart2 := convert(series(E,t,10),polynom) assuming t>0: poss_minpol2 := [seq(k[1], k=sqrfree(res2)[2])]: PE := op(select(p->convert(series(subs(e=serstart2,p),t,5),polynom)=0,poss_minpol2)): PE := collect(PE,e);

 

(8)

 

>	# Solving this quadratic polynomial in e gives a slightly simpler algebraic expression for E E2 := sqrt((25*t^3 - 10*t^2 - 19*t + 4)*(-5*t + 2 + 2*sqrt(5*t^2 - 6*t + 1)))/(25*t^3 - 10*t^2 - 19*t + 4); series(E2,t,10);

 

 

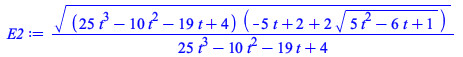	(9)

 

>

 

>	# Note: The gfun package can (non-rigorously) *guess* this algebraic equation directly from the series expansion! seriestoalgeq(series(E,t,30),e(t)) assuming t>0;

 

(10)

 

>	# Instead of the resultant computations above, one can use this guessed algebraic equation, algebraic degree bounds on E from the degrees of r1 and r2, and creative telescoping arguments to rigorously verify the minimal polynomial.